Il Paradosso di San Pietroburgo

Nel quadro del progetto speciale in collaborazione con il Prime-Broker EXANTE Insider.pro continua il ciclo degli articoli di divulgazione scientifica "La matematica degli infiniti e la realtà delle finanze" dal dottore in fisica e matematica Viktor Argonov riguardo ai paradossi della teoria dei giochi e ai modi sorprendenti di applicarla nelle finanze.

A un giocatore si propone di giocare secondo le regole seguenti. Prima il giocatore paga M dollari al casinò (pagamento per gioco). Poi il croupier lancia una moneta. Se alla prima mossa viene croce, il giocatore riceve 1 $. Se croce viene anche alla seconda mossa, il giocatore riceve ancora 2 $. Se vengono continuativamente tre croci - 4 $, se quattro croci - 8 $. E così via in modo esponenziale. Appena viene testa, il gioco finisce. Il casinò si prende M dollari e il giocatore quello che ha fatto in tempo a vincere.

Facciamo la domanda seguente.

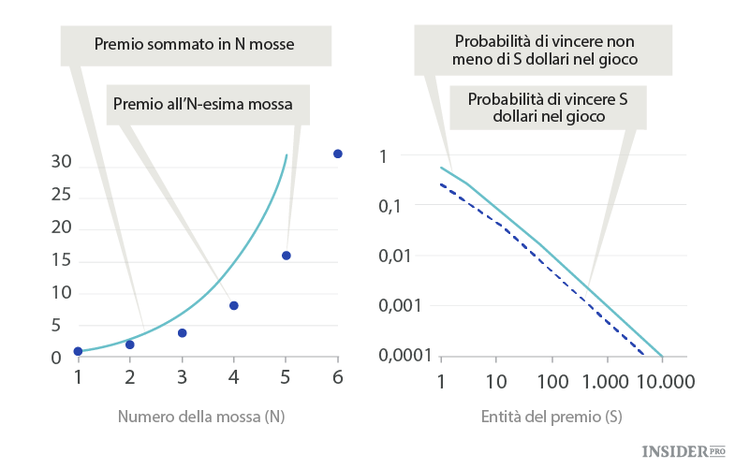
Con proficuo si intende che se gioca un gran numero di partite, vincerà più di quanto ha pagato. Cioè vincerà una somma maggiore di M. I grafici fanno vedere come va crescendo il premio a ciascuna mossa e qual'è la probabilità di guadagnare in tutto il gioco qualche somma (M escluso).

A sinistra i grafici sono in scala lineare. Si vede quanto rapidamente cresce il guadagno durante il gioco. Però anche la probabilità di giungere alla mossa N diminuisce con la stessa velocità. Alla prima mossa il guadagno totale è 1 $ e la probabilità di rimanere nel gioco in questo momento è pari a 1/2. Alla seconda mossa il guadagno totale è 3 $ e la probabilità di rimanere nel gioco è 1/4. Alla terza mossa sono rispettivamente 7 $e 1/8, alla quarta 15 $e 1/16.

Se prendiamo N grandi la probabilità di rimanere nel gioco è inversamente proporzionale al guadagno sommato. Per esempio, con la probabilità di 1/1000 il giocatore fa in tempo a guadagnare non meno di 999 $.

I grafici della dipendenza della probabilità del guadagno dalla sua entità si vedono a destra in scala logaritmica doppia. Così come nei problemi precedenti sembrano linee dritte (funzioni potenza). Vuol dire che si può aspettare un trucco degli infiniti.

Supponiamo che il pagamento per un gioco (M) costituisce solo 1 $. Il giocatore decide di fare 100 giocate. Secondo i grafici, è molto probabile che almeno in una di esse guadagni 100 $, coprendo le perdite. In una giocata su dieci (cioè circa in 10 giocate) il guadagno può costituire 10 $, che sommati faranno 100 $. Ancora in circa una metà delle giocate restanti i guadagni devono costituire almeno 1. $ Il gioco è ovviamente proficuo: il giocatore copre senz'altro il pagamento iniziale e guadagna ben 100-300 $. Se fa 1000 giocate, guadagnerà migliaia di dollari.

Ma quando l'amministrazione del casinò capisce che il giocatore è troppo fortunato, eleva il pagamento M da 1 a 10 dollari. Vale la pena continuare a giocare?

Adesso il gioco non sembra così proficuo. Per esempio, se si fanno 100 giocate, la perdita sarà 1000 $, mentre il guadagno più o meno certo sarà 100-300 $. Ma è una valutazione approssimativa. Se lo può valutare più precisamente? Qual'è la sua entità media se si fa un numero infinito di giocate? Secondo le formule (più concretamente, secondo il carattere potenza della dipendenza della probabilità del guadagno dalla sua entità), la particolarità di questa lotteria è che il guadagno medio è... infinito. Perciò, in caso di qualsiasi M, il gioco è in medio proficuo per il giocatore.

Dopo gli altri articoli questo fatto non è sorprendente: non si sa mai dove appariscano delle soluzioni contrarie. Per esempio, nel problema della rovina del giocatore il gioco era proficuo in caso di qualsiasi pagamento d'entrata. Ma qui il paradosso principale non riguarda gli infiniti, ma la reazione psicologica della gente.

A prima vista l'analisi del problema della rovina del giocatore e di questo paradosso risulti in due cose.

qualunque sia il pagamento d'entrata M.

Però in pratica i due giochi sono assolutamente diversi. Il gioco in cui il giocatore beve e mangia a spesa del casinò, mentre quest’ultimo cerca di rovinarlo, è un gioco immaginato. Casinò reali non tendono di organizzare tali giochi così svantaggiosi per loro (solo come eventi di promozione). Ma la lotteria di San Pietroburgo è un gioco che esiste in realtà. Singoli giocatori e interi casinò organizzano tali lotterie e non le considerano un gioco vantaggioso solo per uno. Importa anche il pagamento d’entrata: pochi consentono a giocare anche con il prezzo di 20 $. Ma perché?

Nelle parti precedenti abbiamo dimostrato che si deve trattare le soluzioni contenenti gli infiniti con massima attenzione e cautela. Abbiamo notato che in realtà la situazione si può rivelare peggiore. Il mercato punisce regolarmente coloro che ignorano previsioni matematiche “paradossali” e trader lo capiscono. Ma la lotteria di San Pietroburgo è un’altra cosa. Le sue previsioni matematiche infinite non importano a nessuno e non succede nessuna catastrofe finanziaria. è proprio questo l’essenza del paradosso di San Pietroburgo.

Ci sono alcune spiegazioni del paradosso, che si possono dividere in due gruppi: quelle tecniche e quelle fondamentali. Le spiegazioni tecniche sono basate sull’imperfezione del mondo reale rispetto a modelli matematici, mentre quelle fondamentali riguardano delle controversie filosofiche sul fenomeno stesso del ragione e sul senso della vita di un essere ragionevole.

Questo gruppo delle spiegazioni è ovvio. Se ne può immaginare tante, ma tutte sono legate alle difficoltà tecniche dell’effettuazione della lotteria in modo completo.

In primo luogo, per guadagnare molto con la probabilità alta, non è desiderabile rischiare, ma fare molte giocate. Quanto più alto è il pagamento d’entrata, tante più giocate occorrono. Se il pagamento per una giocata è 1 $ (il premio è anche 1 $), bastano 20 giocate per ottener profitto. Ma se il prezzo è 10 $ (mentre il premio è sempre 1 $) il numero di giocate necessarie può risultare così grande che il casinò non le permetterà o il giocatore perderà tanto tempo che non vale nessun guadagno.

In secondo luogo, di solito le regole hanno dei limiti taciti. Se qualcuno ha vinto un milione dal partner, quest’ultimo può rifiutare di adempiere le condizioni del gioco, dicendo che non ha più soldi. è molto probabile che anche il casinò si protegga da situazioni spiacevoli.

In terzo luogo, la gente è psicologicamente inclinata a ignorare probabilità piccole, per questo la probabilità di vincere anche un miliardo di dollari con la probabilità di uno su milione non attira una persona se una perdita possibile (ma quasi garantita) massima costituirà almeno 500 $.

Però tutte queste spiegazioni non si possono considerare soddisfacenti. Perché almeno in mente si può immaginare una situazione in cui tutti questi problemi sono risolti, tuttavia anche una persona più intelligente e giudiziosa ostina di comportarsi in modo “ragionevole”.

Per illustrare l'imperfezione delle spiegazioni tecniche del paradosso, mettiamo da parte le regole iniziali della lotteria e le cambiamo per quelle più semplici e rigorose.

Venite al casinò e vi propongono un gioco semplicissimo. Nel pacchetto chiuso ci sono 100 gettoni: 99 rossi e uno verde. Vi propongono di tirarne fuori uno al tatto. Se tirate quello rosso, perdete i vostri beni. Se tirate quello verde, ricevete un miliardo di dollari. Ammettiamo che si è una persona comune del ceto medio, si possede un appartamento, un'automobile, elettrodomestici. Si lavora in un posto comune che vi ha lasciato guadagnare tutto quanto per molti anni di lavoro. In totale i vostri beni costano 100-200 mila di dollari. è molto probabile che sia proprio la somma della perdita. Tuttavia il guadagno medio (la sua entità di un miliardo di dollari moltiplicata per la sua probabilità di 0,01) costituisce 10 milioni di dollari. Supponiamo che il casinò è pronto a perdere (per esempio, organizza il gioco per un TV show straordinario), è disposto a pagare onestamente la somma, e il contratto non contiene nessun dettaglio doloso.

Dal punto di vista matematico, il gioco è estremamente vantaggioso. Dal punto di vista psicologico, tutt'e due i risultati sono abbastanza probabili. La probabilità di 1/100 non è una probabilità piccola da ignorare. La gente compra volentieri delle lotterie comuni con una probabilità di gran lunga più piccola di vincere. Ma nel nostro caso è evidente che la maggior parte della gente rifiuterà di giocare. Tranne emarginati il cui vita non è riuscita (che non hanno niente da perdere) oppure avventurieri patologici.

Questo esempio dimostra che non soltanto la "torbida" lotteria di San Pietroburgo, ma anche un gioco di gran lunga più trasparente con due risultati e un enorme guadagno medio non garantiscono il comportamento "ragionevole" di persone. Non è necessario intendersi della matematica, ma le condizioni del gioco sembrano lo stesso inaccettabili alla gente. Perché?

Dal suddetto discendono logicamente due varianti possibili. Ovvero la maggioranza della gente va riconosciuta scemi (che risolvono in modo sbagliato anche un problema molto semplice), ovvero si deve ammettere che il comportamento ragionevole non è pari alla massimizzazione del guadagno e che il benessere della persona non è proporzionale alla sua ricchezza. è proprio la seconda la spiegazione giusta.

Secondo moltipliche ricerche, non si può dire che una persona che guadagni un miliardo di dollari sia un milione di volte più felice di una persona che guadagni un mille dollari. Dal lato psicologico il gioco con una puntata troppo alta ha un guadagno medio negativo. Per la maggior parte della gente un guadagno di un miliardo di dollari e la perdita di tutti i propri beni sono avvenimenti ugualmente importanti. Poiché la probabilità del guadagno è molte volte più bassa della probabilità di perdere, il gioco viene automaticamente rifiutato. Del resto, ne parliamo in dettaglio nella parte successiva.