Nel quadro del progetto speciale in collaborazione con il prime broker EXANTE Insider.pro pubblica un brano tratto da "La matematica dell’infinito e la realtà delle finanze" di Viktor Argonov, dottore in matematica e fisica, sui paradossi della teoria dei giochi e la loro sorprendendte applicazione nel mondo della finanza.
Nella storia della teoria della probabilità la finanza ha sempre avuto spazio. Per esempio, già nel 1650 gli illustri scienziati Blaise Pascal e Christiaan Huygens si misero a studiare il cosiddetto problema della rovina del giocatore. Ha molte varie formulazioni, ma facciamo attenzione a una di esse, particolarmente paradossale.
Un giocatore compra dal casinò M gettoni, ciascun dei quali costa $1 (i soldi pagati per i gettoni sono il suo pagamento per partecipare al gioco). Una volta al minuto il croupier getta una moneta. Quando viene "testa", si prende un gettone dal giocatore. Quando viene "croce", invece dà al giocatore un gettone. Il numero dei gettoni a disposizione del casinò non è limitato, allora non si può rovinare. Ma il giocatore può. Il gioco continua fino a che il giocatore abbia speso tutti i gettoni. Così non vincerà del denaro: è un gioco in cui uno è destinato a perdere. Tuttavia mentre il gioco procede, il giocatore ha il diritto di bere e mangiare gratis, di chiacchierare con altri giocatori e divertirsi a spese del casinò (non è obbligato a star vicino al croupier che fa tutto in buona fede).
Facciamo quattro domande:
- Quante probabilità ha il giocatore di rovinarsi dopo N movimenti ?
- Qual’è la mediana di tempo del gioco?
- Qual’è la durata media del gioco?
- Vale la pena partecipare a un tale gioco nella realtà e a quale costo?
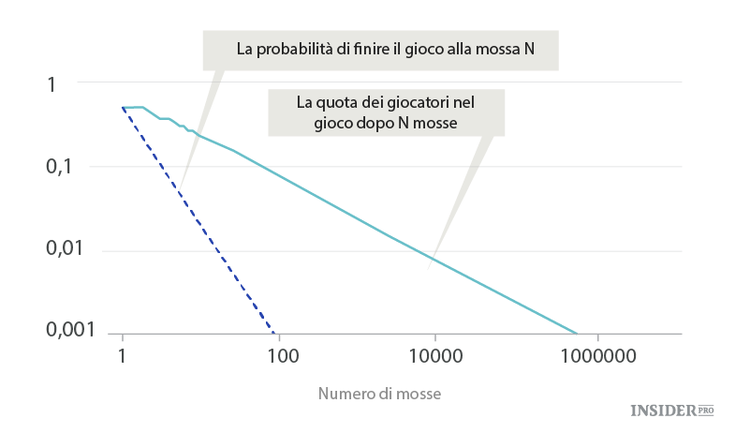
La probabilità di rovina del giocatore diminuisce al crescere di N secondo la stessa legge potenza così come la probabilità del ritorno dell'ubriaco. Anche qui ci sono delle partite straordinariamente lunghe (i voli di Lévy) a causa dei quali il tempo medio della rovina del giocatore è infinito. La sola differenza è che il giocatore non comincia con zero, ma con M gettoni. Perciò il tempo mediano del gioco è allora diverso: è approssimativamente proporzionale a M².
Cosa significa in pratica?
10.000 mendicanti a rovinare il casinò
All'inizio consideriamo un caso semplice: M=1. Un mendicante con $1 entra nel casinò. Il tempo mediano costituisce solo una mossa (con la probabilità di 1/2 alla prima mossa verrà "testa"). Però, secondo le formule, il tempo medio aspettato è pari all'infinito.
Quale rischio comporta al casinò? Se nel casinò non vengono uno o due mendicanti, ma 100, 1000 e anche di più, circa una metà di essi verranno "tolti" alla prima mossa, ma tra i restanti ci saranno dei "fortunati" che costituiscono una minaccia per il casinò. Tra i giocatori c'è una certa percentuale di "fortunati" le cui partite si possono trascinare per giorni, mesi e anni (i voli di Lévy).
Al crescere di N la quota dei giocatori rimasti nel casinò è inversamente proporzionale alla radice da N. Uno su dieci giocatori resta nel gioco circa fino alla centesima mossa, uno su cento fino a quella decimillesima e uno su mille fino a quella milionesima!
Vuol dire che se 1000 mendicanti con $1 verranno nel casinò, uno o due di loro "si stabiliranno" nel casinò per alcuni anni! Se verranno diecimila mendicanti, tra loro ci sarà una persona che avrà il diritto di divertirsi gratis per centinaia di anni! Mentre per la maggior parte degli altri partecipanti il gioco durerà sempre circa un minuto.
Questo problema fa vedere quanto prudenti debbano essere gli organizzatori dei giochi d'azzardo. Non si può sempre valutare "a occhio" quando si parla di profitti e perdite. In un casinò reale si può effettuare il gioco seguendo queste regole, senza divergere dal modello matematico.
Un giocatore con 10.000 dollari rovina il casinò
Se M>1 la situazione può rivelarsi anche peggiore per il casinò: adesso i giocatori non hanno bisogno di un gran numero di partite.
Il tempo mediano è pari a M². Cioè dipende dal capitale iniziale del giocatore così come il tempo del gioco del più fortunato mendicante dipende dal numero dei mendicanti (e dal loro capitale sommato). Non è una semplice coincidenza, c'è un legame profondo di cui parleremo più tardi. Ma prima stimiamo le previsioni riguardo al gioco in casi di M vari.
Se due amici vengono nel casinò e ciascuno punta $10, almeno uno di loro "si divertirà" a spese del casinò per più di un'ora e mezza (il tempo mediano è 100 minuti). Se puntano $100, tutt'e due con un'alta probabilità potranno divertirsi giorno e notte circa per un mese. Diecimila dollari basteranno per "stabilirsi" nel casinò per centinaia di anni (!).
Il capitale iniziale è importante
Non è difficile capire perché i risultati dei "fortunati" mendicanti sono così simili ai risultati delle persone che sono venute col denaro. "I fortunati" sono quelli che grazie alla buona sorte sono riusciti a capitalizzare così tanto da rendere difficile il loro abbandono dal tavolo e la loro rovina. Quanto più alto è salita la persona grazie al caso, tanto più difficile è "farlo tornare sulla terra".
Se nel corso della partita un mendicante è stato fortunato a inanellare 9 puntate fortunate (e ricevere 10 gettoni), il suo gioco seguente non sarà diverso da quello di colui che ancora all'inizio ha comprato 10 gettoni. Per tutt'e due il tempo mediano costituisce 100 minuti. Quello che ha a caso preso 100 gettoni continuerà a giocare ancora per circa diecimila minuti.
Questa conclusione tirata dalla teoria dei giochi ha delle conseguenze importanti. Aiuta a spiegare la disuguaglianza economica nella società e dice com'è importante "il margine di sicurezza". Una società o una singola persona ricca dotata di un gran capitale possono spesso possono mantenerlo per secoli, mentre piccole start-up appaiono e spariscono ad alta velocità. Queste considerazioni riguardano direttamente la dinamica delle quotazioni delle azioni.